Chapter 02
Structural Electrodynamics
SED
There is an entirely new world between our concept of an infinitely small point and the current limits of our imagination. To explore this world, a new model of the atom and its components is proposed based on the dynamic structure of fields, fields that are purely electromagnetic, requiring nothing but themselves as they vibrate rapidly in space-time, forming not only photons of light but all the energy and matter in the universe. Everything.
We will see how these fields create elementary particles from highly energetic photons called gamma rays, plus offer an explanation for the broad evolution of the universe and its early stages of inflation when all this matter was formed.
Given the correct phase, and energy, these photons can superpose and merge to form matter through a process described by Structural Electrodynamics (SED) and a structure called a soliton. This creates matter from energy. These ideas follow Confucius, Maxwell and Einstein. Rhythmic fields of light vibrations, continuously becoming their opposite in space-time and holding their place in a soliton, to portray the quality of mass and inertia.
SED also proposes a completely new and simplified concept of gravity and a unification of the four forces. Much of what is discussed here may initially be surprising for many physicists, as it posits an alternative to their current paradigm, the standard model. Possibly, by using more approachable standard physics, this model opens another window. Take a look. Only time and experiment will show which is the right view.
What is a particle and what is spin?
A modern and suitable definition of a fundamental particle is as follows: A particle is the smallest possible vibration of a quantum field. We will find our model adheres to this definition precisely, being based on one cycle of an electromagnetic wave. That is, there is no sustained minimum or smaller vibration other than this, and the electromagnetic field is a quantum field.
The concept of spin in elementary particles has always been a difficult problem for particle physics because its current theory maintains spin is not real angular momentum but purely an intrinsic or quantum property. This is because it declares particles are infinitely small points with no spatial extent and so there is nothing to rotate. Their argument continues by saying if they had a size, this implies particles would have to spin faster than light.
In contrast, SED theory, with its structural model based on quantum fields of circular motion, proposes that spin and angular momentum are truly identical. Classical mechanics can account for elementary particle spin because spin is a rotation of mass formed from light, and it is the fields that are spinning.
In our model of matter particles, E-M energy follows a tiny path consisting of two circular loops with an exact radius that achieves light speed because it is light and creates all the other fundamental properties including what we interpret as mass and charge. Moreover, being made only from fields means particles are not a solid ball or point, but simply energy and their influence extends beyond their size and continues throughout surrounding space. All particles possess angular momentum equal to exactly one unit of Planck’s constant or h of spin. Fermions or stable particles that portray mass, will be shown to exhibit a half spin or h/2 at any one time in order to exist and create their properties. However, their total overall spin is still h. Just how will be discussed shortly. First though, we need to examine h, the quantum of spin.
SED maintains that the subatomic world is not quite as weird as quantum mechanics makes out and will present its reasons throughout this book. To start with though, we offer some introductory ideas about what an elementary particle is and what it is doing. There have been many explanations put forward by physicists over the years to describe what matter is, most of them complex, abstract and not very succinct or memorable.
Among other things, SED proposes a model that finally answers the dilemma of wave-particle duality. It is the resultant structure of this model due to these fields alone that determines a particle’s properties. Fields vibrate like waves and particles are made from fields when the waves vibrate in a particular manner that holds them in space, forming a special type of standing wave called a soliton.
At the fundamental level two types of particles exist according to SED. There are those that are purely energy (photons) which have zero rest mass and always move at c, the speed of light. These are not solitons and are perfectly flat or two dimensional. The other type is matter (particles). These quantum particles are solitons made from photons that have an overall spin of h, as their standing wave vibrates endlessly on a tiny, fixed path. Because the path consists of two loops, angular momentum is measured as h/2 at any instant in time, first in one loop and then the next. These loops create a volume for the particle, giving it mass or inertia and other properties such as electric charge and magnetism.
This new dynamic model of matter is built on a rotating photon which SED calls a roton. This roton is a unique type of soliton that makes a permanent standing wave in three-dimensions, with a constant form that retains its place in space and does not disperse. It is localised. Normally all spin is flat and exists in only two dimensions. For matter particles though, this spin arises from a combination of two source photons that were spinning at 90º to each other and then superpose. The resultant spin exists in three dimensions, yet it is very stable.
Elementary particles are perfect solitons, consisting of energy supplied by the Big Bang and trapped within the roton. They can survive for billions of years. Many other examples of solitons exist in nature from smoke rings to soap bubbles and slow-moving canal waves. We will explore them in greater detail in upcoming sections.
The Principles of Structural Electrodynamics
1. The laws of physics are essentially the same regardless of the size of the system under consideration. This applies everywhere from galaxies down to the smallest scale of subatomic or quantum dimensions.
2. At the level where Planck’s constant is relevant, all inherent or intrinsic motion is circular, and the minimum (1) quantum of angular momentum is ћ. Linear momentum is merely the case when the radius is large.
By adhering to these two ideas and applying the laws of classical physics to our model, we will show that the properties of all physical things, including matter at its most basic or fundamental level, together with their correct values, may be derived from first principles. For example, the overall magnitudes of both the electric and magnetic fields within the electron are calculated and then used to determine the size of the elementary charge as well as the Bohr Magneton (i.e. its magnetic moment), thus providing self-consistency of the theory. Later we will discuss the similarity between a black hole and an elementary particle due to their structure alone. Even the elusive fine structure constant will be seen to have a new physical basis when considered from this perspective.
We will endeavour to show that the universe is far more connected and unified than most modern physicists admit and that all its interactions stem from a common source. This source concerns the behaviour of electromagnetic (E-M) fields, which physics well knows are the basis of light, but here we will find they are also the basis of every physical thing in the universe. Ultimately, there is nothing other than E-M fields and their interactions in the entire physical world.
Returning to the importance of circular motion, and the reason we say it is the basis of all activities in the subatomic world is threefold. Firstly, this is due to the critical importance of Planck’s constant at this fundamental level. There is no equation in quantum mechanics that does not contains the term h, and h itself is nothing but spin and the manifestation of real and absolute rotation, despite what particle physicists try to tell us. Secondly, these fields have a strength or value that SED will show is determined by a little-known constant called The Magnetic Flux Quantum. This constant defines the minimum product of magnetic field strength and the area through which the field acts. In elementary particles, this area is always circular, and it is the magnetic field itself in the roton that pulls it into a circle. Thirdly and also very significantly, in our larger massive world, circular motion is by far the most common form of movement that exists. Every moon, planet, star, galaxy and galactic cluster exhibits this type of motion, due to gravitational influence on a large scale, although here on the surface of our little planet, while we may experience comparatively larger amounts of linear motion, this is relatively minor overall.
The only motion that sustains has angular momentum. Circular motion.
As we will discuss later, a major new idea within SED concerns what physics terms supersymmetry. This is the process of creating matter from energy or, as it is also known, turning bosons into fermions. The subject of electrodynamics is deeply involved with this. Particle physicists so far have no mechanism to explain it, but we will show how gamma-ray photons made entirely from highly energetic E-M fields, can superpose to form a standing wave of energy or soliton, a stable three-dimensional structure with a rest-mass equal to this energy. It has been called a Hubius Helix or two-turn helix, however SED prefers to call it a roton (rotating photon). All matter is made from rotons, and we will examine their construction now.
Note: Having a demonstration model to build and interact with, such as the marked-up strip shown in Figure 3 below, is an extremely useful aid in following these ideas.
A model of matter - the roton
A model is a simplified (usually physical) explanation of some complex phenomena. All useful scientific models need to meet at least two criteria:
1. They must be self-consistent.
2. For every input given to the model, the output must be real.
The model proposed here is both a shape and a process, consisting of electromagnetic energy flowing on a 3-D path that is infinite yet enfolds a tiny space - the space that matter occupies.
We will consider how two circular motions can combine to form a unique new entity with properties that explain how matter came into existence and how every physical thing in the entire cosmos has their origin in this universal source and structure.
A structure we can readily perceive but until now had not considered.
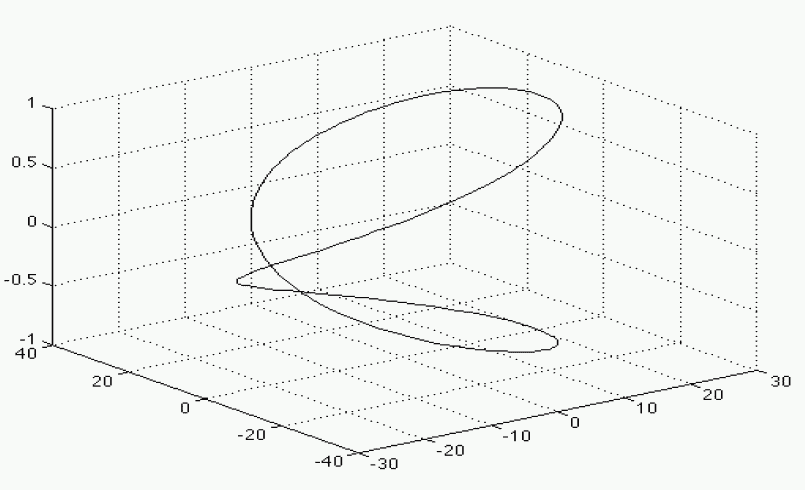
Figure 1 - A roton made from a plastic strip and viewed from the front. Note the two loops.
Figure 2 - A 3D view of the Hubius Helix or roton when drawn vertical. (Thanks to Qiu-Hong Hu) [1]
Figure 3 - A model of the roton made with a marked up plastic strip.
The construction and shape of a roton
The roton is the path that forms the basic structure of these particles. It can be created in several ways, as in the three examples described below. Familiarity with this shape and how it arises is vital to understanding the model and this theory. We again state that the reader is advised to make a marked-up demonstration model themselves to gain a better understanding and familiarity of how the roton works, for without a good knowledge of its structure and properties, this theory may not make a lot of sense(2). The first model involves making a roton from a length of plastic and presents it as a physical ‘thing’, whereas the second and third use more abstract methods to convey how it is made by rotating two circles simultaneously in two different axes at 90º to each other. Fully grasping the concepts behind the roton’s special shape and its properties may be the most difficult idea in this book, but by far the most important.
A thin strip of semi rigid material e.g. a woven plastic strap about 1 cm x 50 cm is twisted one full rotation or 360°, then the ends are joined at the crossover, creating a curved-down infinity symbol as in Figure 4 below. This can be marked-up to show E-M field directions and distinguish inside/outside surfaces as described in the sections on charge and magnetism below. Note: This is not a Möbius strip which has only a 180° twist and forms one continuous surface. The roton has two, inside and out.
Figure 4 - Making a roton from a thin flexible strip. It should be marked-up with a single cycle of an E-M wave to show not only its shape, but directions the electric and magnetic fields take when forming a roton.
Figure 5 below illustrates how rotating a vertical disc (e.g. a CD) in its plane, while simultaneously twisting it sideways in a circular motion at the same rate, forms a roton. The locus of the small pink circle drawn on the disc's edge is the path of the roton. Significantly, rotation direction (i.e. clockwise or anticlockwise when viewed from front) reverses twice each 360º to maintain angular momentum. There are also two, 360º turns per 720º cycle, as is a requirement of Lie groups, and consistent with the spin of fundamental particles and spinors. However, this model does not need any abstract space, regular space is perfectly sufficient. This twist motion prevents the fields changing their sense as will be explored in the sections on electric charge and magnetism.
Figure 5 - Making a roton from rotating discs. The pink dot forms the path of the roton as the discs rotate together.
Figure 6 shows how the same roton, but in this case in a different orientation, can be created by tracing the path a small area on a polar great circle sweeps out, as it rotates around a horizontally revolving sphere. Like a plane flying a polar great circle around the earth every 24 hours and viewed from space. The roton lies on the surface of the sphere in one vertical hemisphere. This has the same shape as in the models above but may be easier to visualise.
Figure 6 - Making a roton from a revolving sphere and a great circle. In matter this sphere has a diameter of ƛ√2, where ƛ is the particles reduced Compton wavelength.
In the last two models we have used a small circle rather than a point, to form the roton’s path because this helps envisage that the twist of the small circle, as it moves around its path, is essential to the creation of the soliton. With the strip model, this twist is more obvious and helps show how the model’s topology enables the standing E-M fields to produce a soliton.
How matter is created – The formation of a soliton
To recap, in our model, a stable particle is a soliton, an enduring standing wave of field energy with a 3-dimensional structure, made from the superposition of two highly energetic, single cycle and flat electromagnetic waves. It spins with an angular momentum of h and its precise energy yields a corresponding mass and volume that is sustained and localised in space-time. Once formed, energy flows continuously at light-speed, along an endless path comprising the soliton, but having acquired mass means it is compacted into a tiny volume, so its group or external speed is always less. All other measurable properties of the particle such as its charge, magnetic moment and particle type (e.g. nucleon or lepton), are directly and simply derived from the electromagnetic properties of this structure, with no need for further assumptions. Most particles were created during the Big Bang, when its extreme temperatures supplied vast numbers of gamma ray photons with sufficient energy. Maybe others are being formed in the hottest regions of the present universe. It is also possible that with future technology, we could do the same.
Supersymmetry is the process of creating matter from energy. It is also how spinors are made for a spinor is simply a roton. We will devote a full section on the physics and construction of spinors in a later section. This section describes how photons can collide and superpose to create a particle.
We begin with the theory of solitons (3). Like Higgs theory which has ‘borrowed’ many of these ideas, a soliton has its minimum energy at a constant non-zero field strength. This minimum is known as the vacuum state and enfolds the soliton, trapping its energy inside. The vacuum state corresponds to a minimum of electrical potential energy and lies on a sphere which geometry shows has the diameter of ƛ√2 or about 1.4 times its reduced Compton wavelength. No other particle can ever penetrate this space because inside this hemisphere field energy immediately rises above this minimum and cannot change. It has only one state and its space is full. This explains why the Pauli exclusion principle prevents the quantum numbers of two fermions being all the same. They cannot occupy the same space-time with identical energy. We will soon see why though, that this is not the case for bosons.
Figure 7 - The dimensions of the roton drawn flat (left), and as viewed from the front when bent down at 90° (right).
Figure 8 - A graphical view of the lemniscate or infinity symbol. Its equation, in polar form, is: r² = ƛe2Cos2θ. When each loop is bent down at 90º from the crossover it forms a roton. Each loop then appears circular when viewed from the side with a radius of ƛe/√2.
Theory also shows that for a soliton to exist we need its field magnitude to be zero at some time, but at that same time, the energy carried by this field must have a definite non-zero value. This occurs in our model at the crossover when both electric and magnetic fields are momentarily zero but keep moving at the speed of light. Now, because intrinsic energy remains constant at mc² = hf = ћω, we have both necessary conditions for a soliton to form, as described in Rebbi’s article [2].
Outside the particle, field strength follows the normal inverse-squared law, as shown in the drawing below (Figure 9). In this way, we see the similarity between an elementary particle and a black hole.
Figure 9 – Potential energy in a soliton forming matter. Its total energy is mc² and its diameter is ƛ√2.
The diameter ƛ√2, forms a kind of event horizon, being the size of the hemisphere which the twisted, two-looped shape, or roton, generates. It defines the location of the vacuum state below which the particle’s energy is fixed and forms a mathematical transition surface, separating internal and external fields. Their ratio is also the fine structure constant. The structure holds energy inside by compacting space using this same ratio and that is why it is a soliton.
How a roton is formed from two photons
A roton or rotating photon can be formed when two gamma rays collide at 90º and superpose as shown in Figure 9 below. Two flat, 2-dimensional photons are required to form the 3-dimensional structure of a roton. Here they combine to form an electron and a neutrino. A neutrino may have a tiny mass and so it is quite large, but it does carry one ћ of angular momentum, just like all elementary particles. The production of a neutrino is needed to conserve angular momentum, with two units of ћ before and after the interaction. It is also involved with energy conservation.
The energy carried in each photon is measured by its angular frequency (E = ћω) and size (its reduced Compton wavelength, ƛ). Without the neutrino, each photon would have an overall path length twice that of the electron, because they would each have half its energy (i.e. twice its wavelength). Furthermore, for the electron, considering the structure of the roton and its two loops, each loop would have a radius one quarter that of each of the flat photons.
This reduction in size of the resultant 3-D particle, formed by the union of two constituent photons is astonishing and has a most profound consequence. For this is how space is miraculously compressed when matter is created, leading to the creation of what we call mass and gravity. We will deal with this further in the upcoming section on gravity. But now it is important to realise that it was only during the early stages of the Big Bang, as this process rapidly unfolded, that any type of 3-D object existed. Prior to that only flat 2-D photons of E-M fields existed, streaming chaotically in all directions at the speed of light. This abundant creation of matter everywhere, along with its increasing gravitational influence and energy storage could be what led to the inflationary stage, or phase of rapid expansion in the universe. We have no other explanation for this. There will be more to discuss on this fascinating topic later.
Meanwhile, returning for now to the actual creation of an electron and neutrino, the law of conservation of energy tells us that due to the neutrino’s production and the fact that it is thought to have a very small but as yet unmeasured mass, each photon must also carry half the neutrino’s mass. This means they would both need to be slightly smaller than without a neutrino being involved. Furthermore, because the pathlength of each loop is half the overall Compton wavelength of an electron and two constituent photons are required to create it, each photon is twice the electron’s size (half the energy). Therefore each loop in the roton (i.e. electron) is fractionally more than one quarter the radius of each of the incoming photons, and its frequency or energy is not quite twice theirs.
Of course there was a continuous range of energies in all the photons randomly flying about the very early universe and only those pairs with the correct phase, energy and direction could superpose to form matter. We will explore this further in the next section on matter and energy, where SED maintains that energy is actually a continuum and only Planck’s constant is a quantum. But because of the energy density and the fact that the cosmos was so hot in the beginning meant that this type of interaction occurred often.
When the two photons collided, each contributed half of the roton’s final frequency, each being responsible for a single loop in its structure. Each loop has only half the resultant angular momentum, or h, of the roton and two opposite loops were needed to form the complete wavelength that became a particle. The two loops rotate at 90º to each other, just like their constituent photons did when they superposed.
As we will show in the section on the electron, the radius of the loops in the roton give us a measure of the electron’s size. We can use this to scale the sizes of the objects in the following drawing of electron formation. Note the neutrino is not drawn to scale because its mass is so uncertain. However, it must be fairly large due to its tiny mass.
Figure 10 – How a roton or particle is formed from two orthogonal gamma rays.
Normally spin or h is flat and exists in a single plane occupying only two dimensions just like all other pure circular motion or discs. At the fundamental level energy is also like this. Our model shows that mass is created in particles when angular momentum or h spins simultaneously on two separate pairs of axes forming a 3-D object with volume.
After the photons interact, any residual linear momentum is taken away by the electron/neutrino pair, due to conservation of linear momentum. Other conservation laws are obeyed as well. Both classical physics and Schrödinger’s equation can be used to track the object. Schrödinger assumed that waves are involved, and they all have angular momentum of h.
Fermions, leptons and nucleons
A roton or elementary particle can be formed when two gamma rays collide at 90º and superpose as shown in Figure 10 above. Here they combine to form an electron and a neutrino. A neutrino has a tiny mass and so it is relatively large, but it does carry one ћ of angular momentum. This conserves both energy and angular momentum, with two units of ћ before and after the interaction.
The energy carried in each photon is measured by its angular frequency (E = ћω) and size (its reduced Compton wavelength, ƛ). Each photon contributes almost half the resulting electron’s energy or mass because each loop in the roton is half the radius of the incoming photons, and so its frequency or energy is twice theirs, due to the finite speed of light. This is not exactly half because the neutrino is thought to have a very small but as yet unmeasured mass.
Leptons are a type of fermion or matter particle that is based on a single roton. The other type is a nucleon which has a more complicated structure due to the fact that it is formed from two virtual rotons. This enables it to occupy two states together. Two types of nucleon exist - Protons and neutrons and they both mostly exist in the nucleus of an atom.
We will discuss this further in the section on The Atom.
de Broglie or matter waves
Once a particle is formed there are two aspects to its motion. The pre-existing internal wave motion where field energy continues to move at the speed of light around the roton’s tiny path, and its new external group motion as perceived from our world on the outside. However, from both of these perspectives Planck’s constant maintains its dominant influence.
We always have ћ = mcƛ for the field’s wave motion in the roton, but now the particle has mass and new equations to follow based on Newton and Einstein’s laws. From our larger view we have angular momentum, L = mvr, and here ƛ is r, the radius of motion or position of the particle, and its velocity is v, as measured by us, which is always less than c.
However, because of wave-particle duality there is still an associated wavelength or ƛ for the particle and this is its de Broglie or matter wave.
Every particle is always a wave-particle soliton, and it is this wavelength ƛ that is used in the Schrödinger equation. For particles in our world that are massive compared to elementary particles or are compound particles consisting of billions and billions of elementary particles and consequently form an object that is so much larger, this wavelength is incredibly small and that is why it remained undiscovered for so long. Even solutions to Schrödinger’s equation give wavelengths that are tiny for elementary particles.
This animation shows a roton - a rotating photon forming a stable wave of energy that creates matter.
note: The black sphere is included only for scale and depth.
(1) We use both ћ and h interchangeably in this book. All circles have both a radius and a circumference related by 2π.
(2) SED has a file that shows how the roton is constructed mathematically from simple circular motion. It shows the roton’s path dynamically with 3-D animation in a free open-source program called Blender A video is also available. See the References section for links.
(3) Refer to the paper: Solitons, Claudio Rebbi Scientific American Articles, February 1979. Ref [2].
The Origin of Everything
(Online Edition)