So spin and twist are not the same. Spin is intrinsic and cannot change without changing the particle. It has an absolute sense that never varies once a particle is formed. It determines charge but not magnetic direction. Twist is induced in the roton and arises when an external influence turns this shape inside-out, reversing magnetism, as in the above diagram.

Spin is constant because angular momentum for fundamental particles is also constant. A boson spins either clockwise or anticlockwise, forming one of two different particles. Its helix is either left or right-handed (i.e. plus or minus h) and always maintains this polarisation. Fermions do likewise, though with a twist, resulting in permanent positive or negative charge in the soliton they form. This is charge conservation and the difference between matter and antimatter. Unlike twist, no external influence can alter charge or absolute spin direction without forming a new particle, because to change spin and charge requires reversing one full unit of h. Changing twist only needs half of this, hence a particle can do this and remain the same particle. Remarkably, our model shows how the uncertainty principle can alter the structure of the soliton and form a new type of particle. Particles that enable an atom to be built.

The formation of nucleons and their transformation

The new particles that utilise the uncertainty principle are the proton and neutron, both nucleons. They are created from highly energetic gamma ray photons but unlike the electron, SED proposes each has two virtual quantum wavelengths or sequential cycles in their soliton’s structure, whereas the electron always has one. It is this property that distinguishes nucleons from leptons.

Figure 22 - Energy flows from loop to loop. Each loop has a radius half the particle’s reduced Compton wavelength, so each loop has angular momentum of h/2 at any instant.

Figure 23 - The two states of a fundamental particle when inverted produce opposite magnetic moments

SED explains for the first time why particles with spin 1/2 (i.e. fermions or spinors) have what were previously considered purely quantum and thus apparently bazar rotational properties. Like all elements of the Lie Group, their formation is a supersymmetric process, producing two turns of 360o per full cycle of 720 o in their structure. It turns flat bosons into 3-D fermions with mass and volume. However, the actual E-M wave in the soliton still has a phase of 360o if only its fields are considered. This model perfectly explains intrinsic spin of fundamental particles, but unlike the standard model, has no need for the artificial concept of an abstract spin-space. Regular space will suffice. Fermions have spin, with real physical angular momentum, as the quantum wave moves at the speed of light within their soliton. For more details please refer to the section on spinors.

The roton’s shape always has two completely symmetrical, but opposite loops in its structure, separated at the crossover by a node which is the centre of yin-yang. Each is constructed with a fixed amount of angular momentum (ћ/2), but this in turn is made from either one of two pairs of physical properties (i.e. momentum/wavelength or energy/time). Furthermore, the separate components in each pair can vary reciprocally, provided their product does not exceed ћ/2. This is the basis of how the uncertainty principle is formulated. It is each loop that has this physical significance or reality, but as there are always two and because they must be opposite, summing or totalising over one full wave would cancel this out. Therefore we only use half in the mathematical expression of the uncertainty principle.

Matter and antimatter

It was stated before that charge arises in fermions due to a left or right-handed spin in the original source photon, and that once created in the soliton, this will not change. The chance of forming either type of charge was almost the same, but somehow it came about that electrons are negative and protons positive, in virtually all the atoms we observe. This is what we call matter.

An isolated system in which all spin directions were opposite to those in our universe is conceivable, and accordingly all known laws of physics would still apply. The only difference is that the roton’s spin direction is reversed and therefore all fields and charges would also be reversed. This is antimatter. There is no need for abstract concepts like moving backwards in time. It is simply a matter of reversing the direction of h in our models.

SED can explain how the two types of matter annihilate each other. This happens when matter and antimatter come into close contact, leaving behind nothing but energy in the form of gamma rays. Gamma rays that were their original source photons.

Due to charge, two solitons may attract, but will only disappear completely if they are identical and oppositely charged. They must align as they would appear to each other in a mirror. That is with opposite structural symmetry. Then their two spins are exactly opposite, and their structures merge, like a cyclone and anticyclone coming together and cancelling each other out. Matter is destroyed completely and converted to energetic gamma rays.

Fortunately, it is a lack of structural symmetry in our bigger complicated world that allows our universe to exist. As evidence of this, we have positrons formed deep within stars during the reaction that is called proton decay, when energetic protons smash into each other, forming neutrons and positrons plus neutrinos. These positrons are antimatter yet can exist inside stars for millions of years. Only when they meet their exact opposite, an electron, near the star’s surface are the two annihilated and converted into gamma rays.

It is well accepted in physics, from both theory and experiment, that matter can be completely converted to energy. Why not then, the reverse? This is after all what we call symmetry in science.

Spin, twist and magnetic moment

Due to external interactions and energy transfer, fundamental particles exhibit twist or inversion, a parity or handedness in their overall shape, that can be swapped once they are formed. This is either left or right-handed but unlike charge, can be reversed, so that magnetic field direction is inverted and flips, turning it inside-out. Only with the right impulse of external energy can the outer surface of one loop become the inside when it flips. Our model shows this reverses apparent magnetic field direction but not charge. Critically, absolute spin direction inside the soliton does not change. Only in a relative sense does it appear to do so. Unfortunately, these two states were originally referred to as spin-up and spin-down and it is likely this naming convention will persist[17]. Nevertheless, we will refer to this externally induced process as twist in the current sections, in an attempt to avoid confusion.

Figure 24 - One roton forms a Lepton (left). Two virtual rotons (one at a time) form a Nucleon (right). A lepton has one state available to it whereas a nucleon has two. Note: The nucleon model is made from a continuous plastic strip that is twice as long as that of the lepton’s. It consists of two cycles.

In this discussion of nucleons and regarding the influence of the uncertainty principle, it is important to distinguish their continuing behaviour once formed, from the manner in which they are initially created or transferred into one another. All existing nucleons, whether protons or neutrons, can continuously change angular momentum during their lifetime but remain the same particle. This ongoing process is purely a virtual twist, without external influence or frequency change and is permitted by the uncertainty principle because it is so small. It allows the existence of one roton or the other with equal probability. This follows a well-known principle in quantum mechanics which states that if something has a definite probability to happen, it will happen. This is confirmed by the two-slit experiment which shows that when a particle has equal probabilities to go through either slit, it will somehow go through both slits.

This is not the case when they are first formed or transferred from one type to the other. A new structure is created then, though this happens only once. An external influence initiates this change, providing energy and spin to create or change the nucleon type. Consequently they are separate particles then, with new charge and the uncertainty principle is not involved. We will investigate this idea further for both the proton and the neutron.

Despite their large energy and size difference, the electron and nucleon are based on a similar shape or roton. In the case of the electron, the path consists of the same single quantum wavelength endlessly cycling in the soliton. However for nucleons, and due to quantum uncertainty, the path can split into two inside-out images inverted at the crossover. Somehow the quantum world permits this behaviour for which we have no equivalent in our larger environment, but many other comparable examples have been observed in experiments. Just why leptons do not do this is something that SED that suggest could be due to their larger size.

For nucleons, energy flows around the roton creating opposite fields sequentially in each loop. At the crossover field values are momentarily zero, and after a full cycle at this node there is a choice of two equal probabilities in the form of two rotons. In quantum mechanics this is called a superposition of states, where energy in the form of a quantum wave can somehow exist in both. Although angular momentum reverses when moving to another roton or state, this is permitted by the uncertainty principle, as they form one of two virtual states. It’s happening at the level of Planks constant and hence its allowable. And because they have identical probability, both rotons in a nucleon are as real as each other and can therefore co-exist. There are two possible versions of soliton that form this stable structure, and we will examine each in turn.

The Proton

In the case of the proton, our model shows that when the paths of the two rotons are continuous and made from one double-length strip joined at the crossover, charge remains constant and positive[18] in both rotons because the electric field in all loops always points out of the soliton’s two hemispheres as shown by the four black arrows above. However, because it is one single path, topology also shows the wave turns inside-out when swapping rotons, and its magnetic field direction is now opposite in each. Note: In the picture above, magnetic field direction symbols (two dots and crosses) are seen on the outer surface of the front roton and inside surface of the rear, which means they are actually opposite. Because of this, the magnetic moment of a proton, µP, rapidly rotates with each cycle, generating an average measurable value somewhat different to that of a Dirac particle[19] (i.e. a simpler, electron-type particle or lepton that has only one state and therefore a constant µ). Very accurate experiments have been performed to determine this difference and it is hoped that it and a future theoretical value based on this model and the oscillating frequency of the proton will agree.

Note: It was this discrepancy and inability to explain how a proton could have a structure somehow different to that of an electron[20], that originally gave rise to the idea of quarks.

The evidence for quarks does not exist. If a future calculation and our model can show how this experimental value is derived, due to such rapid rotation in a close parallel location, we may find the whole concept of quarks no longer necessary.

Figure 25 - The Proton. Here electric field is shown with the black arrows and magnetic field with dots and crosses. The black arrow with the line at centre marks the start of the wave. Note: The two rotons are formed from one continuous strip which turns inside-out when forming a new roton

The Neutron

The other type of nucleon, a neutron, is very stable when inside the nucleus but not a perfect soliton when free and isolated. It only lasts about 15 minutes before decaying into a proton, an electron and an antineutrino. Furthermore, a neutron has slightly more mass than the combined mass of a proton and electron, suggesting these may be its components, together with some additional form of energy that gives it its structure. After performing experiments on earth and observing their formation in the sun, we also know that a neutron can be made from a proton in one of two ways. Either through electron capture, or by giving the proton sufficient energy until it spits out a positron, a positive antiparticle. In both cases, conservation of charge and angular momentum must always apply. Particle physics has used the abstract concepts of isospin, heavy bosons and the weak force to try and explain these transitions. Can SED and our model provide a more direct physical account of this behaviour?

We have discovered how a proton might utilise the uncertainty principle and allow two virtual quantum wave cycles or rotons, to exist side by side in a new structure that differs from leptons. Symmetry shows each roton has the same probability, making a stable soliton that has a constant positive charge, and a special magnetic moment. With only a simple adjustment to this model, we will see how it predicts that nucleons can transform into one another. Nature should be simple, especially fundamental particles.

Reshaping our model with its continuous double-length strip shows that if either of the proton’s rotons is made to rotate through 90°, until the two rotons are orthogonal, this results in a kind of cross[21],and a new structure is formed. Under the right circumstances, the proton could do this by incorporating an energetic electron into its structure, thereby creating a new particle. Once formed, the rotons become two equally probable states, like we have in a proton. However, our model shows one virtual roton creates positive charge and the other rotated roton is now negative. This leaves it electrically neutral, just like a neutron. Again, this occurs in our model, because the strip is continuous. It shows how this action must invert the spin to make the new orthogonal roton. Something that could happen after electron capture by a proton, or almost the reverse, during a positron’s release from a highly energetic proton. During this second process, a neutrino must somehow be captured by the proton, to conserve its angular momentum after the positron’s release. Both interactions cause a significant change in the soliton’s structure, creating a new highly stable but not quite perfect neutral particle. As a result, the neutron is as real as the proton.

We know that a free, isolated neutron is not completely stable. It breaks down into a proton and an electron with the release of an antineutrino after about 15 minutes. When you consider how many vibrations that is, you might think it’s fairly stable, but in the scheme of things it’s not. Only inside the super high energy, chaotic and dense environment of the nucleus can it survive virtually permanently. All the interactions keep it more stable there. However, it’s not the weak force that initiates neutron decay, or its production, for SED contends the weak force is a fabrication, due to imposing the wrong symmetry on a system of forces. We will see later that SED offers a new theory that unites the so-called four forces into one.

A proton can only transform into a neutron when an external electron is involved. Our model shows how. In order to become orthogonal, the roton that turns (in the case of the figure above, the rear one) does not simply rotate by 90°, it must additionally reverse its spin[22] and thus its electric field direction. The two rotons then exhibit opposite charge. Again, this is due to topology and because the soliton’s path must be continuous. It happens only once when the neutron is first formed and is something not allowed if it were free and isolated. Only with the integration of an electron into its structure, and the release of an antineutrino, can a proton transform this way. This is why a neutron is a composite of a proton and an electron. Its creation requires precise energy and angular momentum as well. The neutrino supplies a unit of h, though an antineutrino takes any excess h away using its reverse spin when a neutron decays. Energy can be more of a continuum, but due to the fixed mass of the particles, definite values are required as well. Provided conservation laws are followed, this transformation can also be reversed, producing both neutrons and protons from each other, with other particles emitted or absorbed accordingly. Again, once formed angular momentum is always changing within a nucleon, but never by more than the uncertainty principle allows, so both reactions create physically legal particles.

In neutrons the two virtual magnetic fields are now orthogonal, subsequently they retain an overall magnetic moment, µN., slightly different to µP. and additionally different to that of a Dirac particle. Like that of the proton, the resultant magnetic field oscillates rapidly, making its average theoretical value difficult to calculate, but somehow this must be done. Intriguingly, geometry hints that it must be less than the proton’s by a factor[23] of √2, which agrees well with the two experimental values for nucleons.

Using SED we will see how these two related structures enable nucleons to bond together tightly in the nucleus and form all the different elements. This takes place through the close-range action of the electromagnetic force alone, without the need for a separate strong force. The two variants in the soliton’s structure (proton and neutron) are essential in achieving this. We will furthermore see how they combine perfectly to make all the atoms in the universe, as well as the unique structure of an alpha particle, the most stable of all nuclear composites.

Figure 26 - The Neutron. Note how the electric field (black arrow) points out in the front roton and into the hemisphere in the rear, making it electrically neutral. This is because it is made from a single strip or continuous path

How an atom is constructed

An atom is made with an electron and a nucleus. The electron is a wave that resonates in the atom. The nucleus is like the sun, with smaller waves inside but there are no planets, no hard things orbiting. Just fields in motion, minimising energy to exist. As always.

An electromagnetic clock.

There are over one hundred different types of atoms. The most common and simplest is normal hydrogen, where the much smaller proton is surrounded by a single electron, spread-out into a hemispherical shell. This has the shape of the electron’s soliton (also a hemisphere), as shown in the previous overview section, but randomly orientated and enlarged by 137[24] times due to its lower potential energy. Another hydrogen atom can combine with this structure, provided its electron has opposite spin, to make the molecule of hydrogen, H2, which is generally more stable than the single atom, due to the stability of its fully spherical shell. The simplicity and symmetry of this structure gives the hydrogen molecule its durability and prevalence. It is the most common structure in the universe.

Figure 27 – Hydrogen atom (left), with one proton and one much larger electron. Its hemispherical shell (roton) can be oriented in any direction and accordingly appears spherical. Hydrogen molecule, H2 (right) with its more stable and truly spherical shell

The size of a hydrogen atom is significant. Like all fundamental particles, the electron’s wavelength is inversely proportional to its energy, and its total energy decreases when next to a proton. It has a lower electrical potential energy, and therefore the electron’s size grows by 137 when in hydrogen. The size of this sphere is the Bohr radius of hydrogen and corresponds to this energy change compared to a free electron. The electron is not a point that moves in an orbit with this radius around the proton. It is the complete wave lying on the surface of the hemispherical soliton that randomly envelopes the proton forming the first half of a spherical shell or the 1S orbital. Because the electron is now in a lower minimum energy state, being as close as possible to a proton, it actually relaxes and vibrates with a larger wavelength, due to this lower energy and larger size. The Fine Structure Constant, or α, is the exact ratio of this quantity compared to its energy when free and isolated. It is also the ratio of the size of its two wavelengths in each orbital. Orbitals are a well-established concept in physics but to SED they are just another type of soliton that takes on different sizes and shapes according to its energy.

Two electrons can complete the first shell when two hydrogen atoms combine to make a more stable hydrogen molecule. Each one is a wave function with a unique set of quantum numbers, which means that each captured electron must exist in its own separate state. This means only one specific electron is allowed per orbital, or two per shell when each has opposite spin. We will see later why electrons must have opposite spin in order to co-exist as two orbitals in a spherical shell. Again, this is simply what a soliton does, being a wave trapped in space.

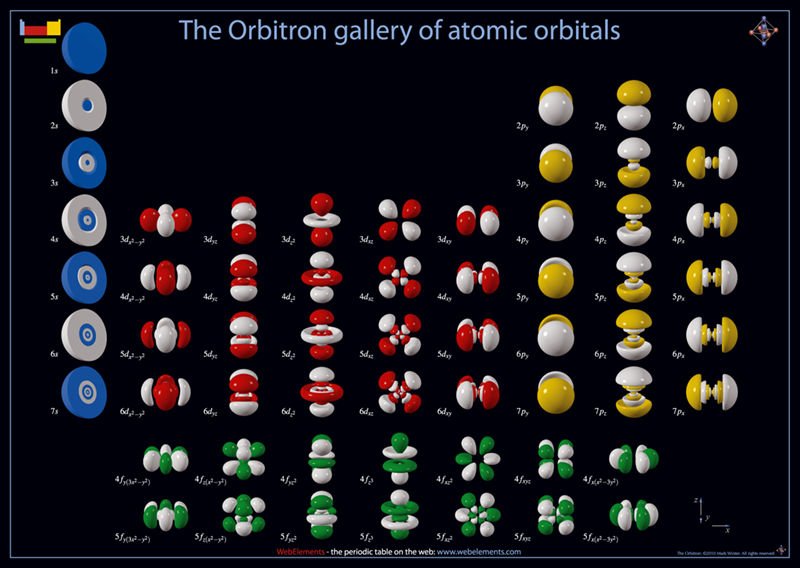
The helium atom has the same spherical shape as a hydrogen molecule but has two additional neutrons in the nucleus. It is incredibly stable and unreactive. All other electron orbitals for the hundred or so remaining elements are likewise based on the shape and structure that is allowed for roton according to its energy. For instance: dumbbells, discs, rings, and larger spheres are further examples of the soliton’s shape when it spins, rotates, or stretches due to different energies, as bigger atoms are built from more electrons and nucleons. SED insists that orbitals are not a cloud formed from a point electron, but actual real solitons, created by the whole wave of E-M energy, that conforms to the environment in which they exist. For a graphical picture of these solitons or orbitals see Fig 28 below.

Each new atom follows the laws of quantum mechanics as successive and heavier elements are created. Their structure is well known to science and is commonly used in Chemistry. It needs to be stated here though that atoms are not elementary particles. They are composites that are made from them. It follows that an atom with more mass will generally be larger than one with less, to accommodate more subatomic particles and their different solitons. We see how atoms become more complex as their atomic number increases, yet their structures always conform to these laws.

Figure 28 – The different shapes of electron orbitals in atoms. Each orbital is a soliton. Thanks to: The Orbitron ©2002-2021 Prof. Mark Winter (University of Sheffield) [6]

What holds an atom together?

The immediate and sufficient answer is the E-M force alone. No other forces are required. However, we will see that the interplay between this force and the fundamental structures, gives rise to two seemingly different sets of properties or behaviours within an atom.

There are two regions where this force is exhibited, inside and outside the nucleus. Due to scale and structure it behaves differently in each, but for the different particles in an atom it is always and only electromagnetic.

Outside the nucleus, the well understood force between the electron and proton holds the largest region of an atom together, for charge is the dominant factor in this space and beyond. On this scale we observe that opposites attract with an inverse distance squared relationship, as elementary physics readily confirms. Of course, electrons repel each other here and obey quantum mechanical rules, with a single wave function or soliton comprising each orbital.

Inside the nucleus, perhaps the most energy dense region in the universe, things behave differently. Nucleons rage in fury and it is what we shall refer to as equals, and not opposites, that now attract as a result of electromagnetism. In the chaos, charge is somewhat irrelevant as solitons briefly align their gigantic fields and almost touch each other to minimise potential energy and create an attractive force, so incredibly strong, that it balances their enormous kinetic energy. This extreme energy density is why the nucleus is such a potential powerhouse for humanity. However, the true source of this force remained a deep mystery even though it had been given a name. Now SED reveals its origin.

What really is charge?

After a single proton, the next simplest stable nucleus comprises one proton and one neutron. These tiny dynamic structures moving near the speed of light, hold enormous energy in their fields and motion, yet somehow remain trapped together in a very small volume. Even protons are attracted to other protons when in this range, despite their repulsive charge, but why do nucleons attract?. The answer lies in the E-M field’s strength, oscillation and structure on this incredibly small scale, as they fleetingly approach and almost touch each other.

Until now physics has always maintained that opposite charges attract. While this certainly seems to be true in our everyday world, it is not the entire truth. If we want to understand why, we need to look in detail at the fields themselves and how they interact. Field direction is the key because in order to attract, fields must line up with each other and be parallel in space. This minimises their potential energy. In other words, they must align and be equal. Equal in the sense that they point in the same direction and have similar strength. If they point towards each other and are antiparallel, they are opposite and will repel. Even in our larger world this is fundamentally how electromagnetism operates, but for some reason has been overlooked. Opposite charges share equally directed fields in space, and it is these equal fields that attract due to their alignment. Our concept of charge is simply a convenience to help understand electricity. We tend to think of charge as a kind of tiny source of static electricity, but by definition it is actually the fixed ratio of the force to the field producing that force, and due to fields alone, as the next diagram shows. Only because of the field’s interaction in the space surrounding particles, do they experience attractive or repulsive forces.

Figure 29 - Attraction and repulsion arises from equal and opposite fields in space, not what we call charge.

Therefore charge is the amount of force the field produces, and it is this ratio that is a quantum. This means that both can vary provided they have a constant quotient. Both can be extremely large or both very small. In our world we often experience the force electrons create and call this the elementary charge. Of course there is only this one value of charge, but if the field is huge, like in nucleons, so is the force, and yet charge does not change. It remains elementary.

Nucleons, which basically are just fields, are attracted strongly to each other when their fields are momentarily in this sense equal and at their closest point of contact. That is when their soliton’s fields are at a maximum, several million times larger than those in an electron, because nucleons are very much smaller. We need our model to guide us here and reveal this significance. It shows that, at this short-range, there is no need for a separate and artificial entity called the strong force. It is simply electromagnetism. The concept of charge is more elusive than we often realise.

We must first understand the geometry, structure and scale of a nucleus, to appreciate these ideas. Nucleons are formed from a pair of virtual rotons lying on two hemispherical shells, joined at their crossovers or nodes. Protons have these shells back-to-back in the same plane, while neutrons have one shell rotated a quarter of a turn, making them orthogonal (See Figs 21 & 22 above). No other particle can penetrate these nucleon’s spaces, but they can come close because of their confinement and high energy inside a nucleus. Depending on geometry and phase, a nucleon can share one or up to four bonding sites this way, where the attraction is momentarily maximum, because each roton has two peaks of field strength per cycle, and there are two virtual rotons in each nucleon.

All nucleons are of similar size, and when their separation is about this same amount, a peak of field in one can almost touch the corresponding peak in another. If their fields are equal, they can align in space and create an extremely strong but momentary attraction. Due to their high energy and frequency, this happens often. Because they are very close, this gigantic force operates on a distance scale smaller than electron charge does, which involves two of these sites at each tip of the roton, where fields peak. However, due to phase considerations and the finite speed of light, they are not simultaneous then, and two separated particles only respond to each other’s average charge from a larger distance. That is why conventional charge is not as important inside a nucleus, where this field sharing aspect of electromagnetism dominates, moment by moment. This is the reason why the so-called strong force is short ranged: it is simply a matter of scale and geometry of the roton.

Physics shows that, to approach each other this way, two rotating objects must spin in opposite directions, otherwise their closest points of contact are moving against each other, like the edges of two equally spinning tops. For nucleons, this is forbidden because the relative speed of light at their nearest points of contact would exceed c. To avoid this, one particle’s loop must spin clockwise and the other anticlockwise, or spin up and spin down, so that where they nearly touch, the comparative speed is zero and in the same direction. Our model shows how this can be achieved.

This is also why electrons must have opposite spin in order to co-exist as two orbitals in a shell, as mentioned earlier. They must conform with relativity.

Figure 30 – Zoomed-in view of two nucleons with opposite spin. When two different loops are close to each other and have equal fields, they attract with an enormous force.

This behaviour is very short-range and extraordinarily strong, created by both electric and magnetic forces that are the result of huge fields[25], pulling the particles together and balanced by their rotational or centripetal kinetic energy. Electric charge is only significant in the largest nuclei when its cumulative effect can become more pronounced. Unaware of this structure and its mechanism, particle physicists were puzzled and simply called this behaviour the strong force but had no physical explanation of its cause. Without a model to guide them, they only knew it was short-range and linear but insisted it was not electromagnetic and subsequently had to be a new and separate force.

SED shows how all nucleons are attracted to one another at short-range, purely by the E-M force. Protons and neutrons alike, moving at speeds approaching light. Their large fields rise and fall sinusoidally, but when equal and close, can provide the great strength required to form a nucleus and hold the particles together to build an atom.

It could not be otherwise in this collection of nuclear particles, for if the attraction came about due to opposites, no more than half as many members would contribute to holding this set together. Only if an attractive force comes about because some property is equal, can each particle participate in a force with all the other members, albeit at different times. This is another reason for its strength. It is the only way such a strong force can manifest universally throughout the densely packed and highly dynamic nucleus.

Each nucleon is composed of spinning dynamic E-M fields that we will find are gigantic, due to the fixed value of a little known but vital constant, called The Magnetic Flux Quantum, Ø0. This is the minimum quantum of magnetic flux that can exist. Flux refers to an area of field (i.e. BA, where B = magnetic field strength and A = area), and is directly related to Planck’s constant, h, and electric charge, e, through its definition: Ø0 = h/2e. It is an important concept, often used in technical electromagnetic theory, yet has largely been ignored by particle physicists. In the previous section on The Electron, this constant was introduced to calculate the size of the electron’s fields. Now SED will use it to determine the enormous strength of the E-M fields inside a nucleus.

Because we know the mass or energy and thus the reduced or radial wavelength, ƛ, of each nucleon, we also know the area of each loop in their roton. This is proportional to ƛ2. As nucleons are a little less than two thousand times smaller than electrons, their field strength must be nearly four million times larger, in order to keep Ø0 constant – a huge increase and furthermore the reason why leptons do not participate in what is called the strong force. It is simply structural. Their much larger wavelength and lower energy prevents them from closely approaching nucleons and interacting this way. An electron can get no closer to a proton than fine structure allows, an enormous distance compared to nucleons. Electrons exist as larger rotons in the space surrounding the nucleus and are attracted to it only by the much weaker manifestation of the E-M force, opposite charge[26], as we have previously perceived it.

The alpha particle

The alpha particle contains two protons and two neutrons and forms the nucleus of helium. When a heavy element with a large nucleus breaks down or decays, it invariably spits out an alpha particle in an attempt to obtain stability and lower energy. This is termed fission. An alpha particle is one of three products of nuclear decay, the other two being a beta particle or electron, and a gamma ray photon, both fundamental particles.

SED proposes a simple model for the alpha particle that could give it its lasting stability. Even though the real particle is highly dynamic due to the enormous amount of trapped energy held in such a tightly confined space, the strength and symmetry in its fields in this model may keep it together as a compound particle. The diagram below shows how the nucleons can momentarily form a circular structure with immense strength and a much lower potential energy, that gives the alpha particle its durability.

Figure 31 - The alpha particle formed by momentary but powerful attraction between two protons and two neutrons

It is the strongest and most stable of all the multi-solitons because it utilizers the largest fraction of bonding locations per nucleon (each of the particles can bond at two of four possible sites). Its structure consists of two neutrons and two protons here shown momentarily side by side, forming a symmetrical ring. Note: Here the rotons and their interactions all conform to the previous ideas described above, regarding charge and spin direction.

Heavier elements

After helium, elements become more dynamic and complex in structure, but their nucleons still bond in the same manner.

We have discussed how both protons and neutrons could have been formed in extremely high energy environments, such as occurred in the Big Bang, when gamma rays collided and superposed to form matter. These are the components of all nuclei. Electrons were formed in a similar but simpler manner from less energetic photons. Together, all these particles can combine to make atoms. As heavier atoms are built from these three stable ingredients, the number and type of nucleons do not always follow a regular one to one formula, although protons and electrons do.

Like their parts, new atoms are only constructed in high energy locations like stars, Generally, stars are made from great volumes of hydrogen gas that is compressed and heated by its own gravity, until it reaches a critical temperature when it self-ignites into a hydrogen bomb, forming helium and energy from the process we call fusion. This is how and where the simplest and lightest elements were formed. The heavier elements required even higher energy environments called super-nova, that are only created during a star’s collapse or ultimate burn-out.

Neutrons and protons need to collide with high energies to combine and form a nucleus. This is what the stars provide but it may often have been a random process. Sometimes more neutrons entered a nucleus than protons, but still the result was a stable form of matter.

Because neutrons have orthogonal rotons, this allows another plane or dimension for bonding to occur and provide more options in the larger 3-D structure of heavier nuclei. It is why they are referred to as a type of moderator in nuclear physics. Any single element generally has more neutrons than protons, not simply because a proton carries conventional charge, but also because of the greater structural variation and hence stability, this entails. The number of neutrons can vary in the same element, providing more bonding sites and we refer to these as isotopes. Again, it is their structure that matters.

Figure 32 - Multiple nucleons in heavier elements. The orthogonal structure of neutrons allows different planes to form. Note: Nuclei are very dynamic, and this is only a momentary view

Concluding remarks

What is an atom? How is it constructed? Why is it incredibly stable?

These are some of the questions addressed here. SED proposes that structure and how it behaves gives us an answer. To help persuade, it might be necessary to take a plastic strip (or several), mark it up, then play with it, as described in the overview. Perhaps, you will then be convinced and agree that the simplicity and beauty of this model holds a truth that makes it so appealing. But remember, the strip is not a ‘thing’, it only represents the path of light, like the flightpath of a plane on a map. Maxwell and Einstein hold the key to its navigation.

[15] Compton wavelength refers to the size of a photon with equivalent energy

[16] Normal hydrogen is the exception and does not have a neutron

[17] Rather than twist up and twist down

[18] For the antiproton, where spin is reversed, this charge is negative

[19] That is one for which µ = eh/2m where µ is magnetic moment, e is elementary charge and m is mass. For a proton, experiments show this is about 2.8 times this value

[20] That is, if they were both infinitely small points

[21] Like a four bladed propeller, with two pairs or hemispheres facing opposite directions

[22] An actual model in the hand confirms this. They are not two separate rotons but one continuous path

[23] The neutron’s magnetic moment is about -1.9 times its Dirac value, giving a ratio of ~1.4 or √2 for the proton’s to the neutron’s values. Magnetic moment for the two particles is turned at right angles in the second loop creating the factor of √2 , using Pythagoras’s law.

[24] This number is commonly known as the inverse of The Fine Structure Constant, α

[25] Their fields are millions of times stronger than those in an electron. The electric field is much larger than the magnetic field. Their ratio is c, the speed of light

[26] On very rare occasions, when given sufficient energy to reduce its size, an electron can be captured by a proton and form a neutron