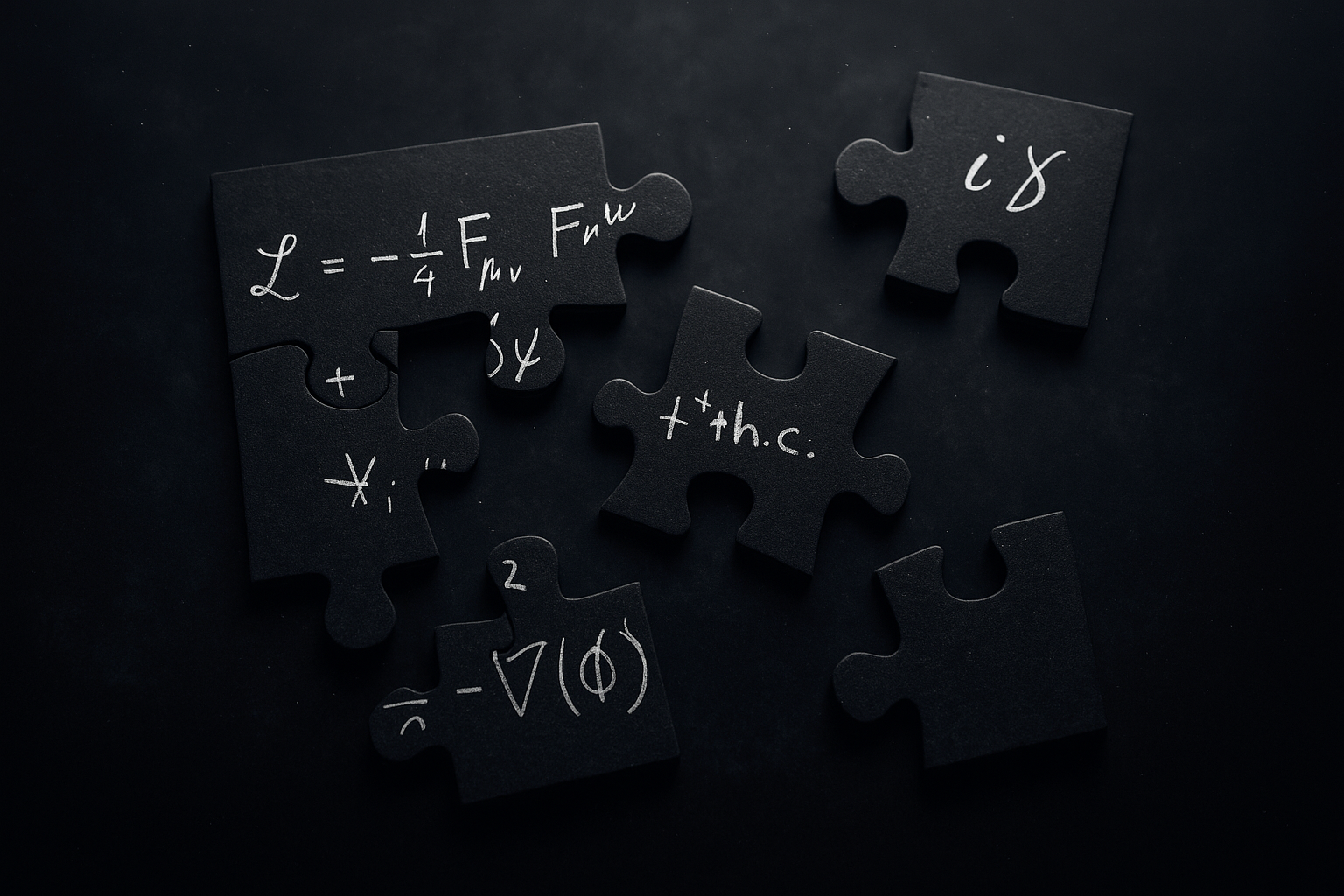Since its discovery in 1916 by Sommerfield, the Fine-Structure Constant, α, has long been a mystery, known precisely but not understood. SED proposes that α represents the ratio between the width of a particle’s electromagnetic path and its overall wavelength, giving physical meaning to this dimensionless number. In this model, particles are structured as twisting electromagnetic fields (rotons), and only a specific internal twist, equal to α, can sustain their stable motion. Thus, α emerges naturally from the geometry of light trapped in matter.

An eternal twist woven into the fabric of every particle. SED reveals that this motion isn’t abstract or symbolic, but real angular momentum born from the spiraling dance of light itself. Through the geometry of rotons, matter inherits its spin, mass, and dual magnetic states. What quantum theory once shrouded in mystery, SED brings into view with clarity and elegance.

The Standard Model claims to explain the fundamental particles and forces of nature - but SED challenges its complexity, contradictions, and reliance on unverified entities like quarks and gluons. What if mass, charge, and spin emerge from elegant field structures instead of patchwork theories? This chapter invites you to question the orthodoxy and discover a simpler, more unified picture of the universe.

What if all the forces of nature - gravity, electromagnetism, the strong and weak nuclear forces - were just different expressions of a single phenomenon? This chapter presents SED’s radical proposal: that electromagnetic fields alone are responsible for every interaction in the universe. From the binding of atomic nuclei to the warping of space-time, SED reveals how geometry, spin, and field dynamics replace the patchwork of separate forces. It’s an elegant unification, long sought by physics and perhaps, finally within reach.

De Broglie’s bold idea that all matter behaves like a wave helped spark the quantum revolution. SED brings it vividly to life. By connecting wave-particle duality to real spinning fields, this chapter reimagines de Broglie waves not as abstract probabilities, but as tangible, physical motion. Discover how the dance of spin, wavelength, and momentum shapes both the quantum and the cosmic.

Spinors are essential to modern physics, yet their physical meaning has remained obscure for over a century. This chapter explores a new perspective from SED that connects spinors with the structure of matter in a clear and testable way. It shows how their strange properties (like requiring a 720° rotation to return to their original state) can be understood as real features of the particles they describe. The result is a model that links the abstract spinor to the familiar electron, revealing them as one and the same.

A sine wave is circular motion viewed side-on. Fundamentally light is always spinning. This chapter explores how the orientation of that spin gives rise to different types of polarisation: vertical, horizontal, and circular. SED reveals how aligned spins in photons unlock phenomena from sunglasses to 3D cinema. Discover how polarisation offers a window into the deeper structure of light itself.

What exactly happens when we measure something? In classical science, measurements were thought to simply reveal fixed properties - but quantum physics reveals a deeper truth: the act of measuring can influence the system itself. This chapter explores how observation collapses possibilities into outcomes, and how uncertainty sets limits on what we can ever truly know. A fascinating look at the fine line between potential and reality.

What does it really mean to observe something in physics and why does it matter? This chapter explores the observer’s role in transforming possibilities into actual events, especially at the quantum scale. From photons emitted one by one to the mysterious collapse of the wave function, it challenges the idea that observation is passive. Is the observer merely watching, or are they fundamentally shaping what unfolds?

Often described as a measure of disorder, entropy is a slippery but fundamental concept shaping our understanding of the universe's fate. From the quiet structure of living systems to the chaotic drift toward cosmic “heat death,” this chapter explores entropy as both a mathematical idea and a deep physical truth. Is energy the driver of disorder? Can entropy itself be stored? These provocative questions are explored further.

Schrödinger’s equation describes how quantum systems evolve, but SED reveals the physical origin behind the maths: spin. Matter waves aren’t abstract- they emerge from the rotational motion of energy in soliton structures. Spin, encoded in Planck’s constant, is the heartbeat of matter itself. This chapter bridges wave mechanics and real structure, grounding quantum behaviour in electromagnetic motion.

Neutrinos are the ghost particles of the universe - abundant, fast, and almost invisible to interaction. SED suggests they are oversized, low-energy rotons with hidden structure and a single unchanging spin. Their mysterious ability to morph between three types may be tied to motion through the three dimensions of space. Could their elusive nature be due to an undetectable charge and giant size? This chapter explores the particle that slips through almost everything, including our understanding.

Are the waves in quantum physics real, or just mathematical ghosts? SED argues they’re electromagnetic through and through - real, measurable, and the very essence of matter. This chapter challenges the Copenhagen view, rooting wave-particle duality in structured energy, not abstract probability. What if potential is more physical than we could imagine?

What makes mass resist motion? And what makes it attract other mass? This chapter explores the link between gravitational and inertial mass, proposing they stem from the same origin: space compression during matter formation. Using the SED framework, it offers a tangible geometric explanation for inertia and gravity, and hints at the futuristic possibility of anti-gravity. Could mastering the geometry of space lead to revolutionary new motion?

Is energy truly quantised? This chapter challenges a core quantum assumption, proposing that while Planck’s constant (h) is quantised, energy itself flows as a continuum - its apparent granularity an illusion shaped by the frequency of vibration. Photons may arrive in discrete packets, but the underlying fabric of energy can take on any value. What determines a particle’s mass or energy? The search for deeper balance continues.

A new beginning is formed. From conclusions on the formation of matter, gravity, and the fine structure constant a new picture of the universe has been defined. Where to from here?

These are the areas where further investigation is needed to complete the Theory of Everything.

Interested in further reading? These are the previous authors and books that helped to form the theories within The Origin of Everything

Before diving into the main content, read here about the motivation behind the book and the big questions it seeks to answer. See who inspired the work, and the thinking that led to this theory, and why it might just change the way we understand the universe.

Modern physics often buries insight under complexity. The theory outlined in The Origin of Everything offers a return to simplicity and a new vision of how the universe is built. Written for curious minds, it presents a bold, unified theory of everything - grounded in known physics, inspired by new insight.

Here we meet the core concept of the book - Structural Electrodynamics: matter is made from energy loops, not point particles. These loops, called rotons, are electromagnetic structures that trap energy in a spinning, three-dimensional wave - a soliton. SED offers a unified framework that can explain particles, forces, and even gravity from first principles.

This chapter redefines the boundary between energy and matter. Energy flows in flat, fast waves, but when curled into a tight loop, it becomes mass. Using this model, we see that light and matter aren’t opposites but two states of the same underlying field.

Quantum physics seems weird only when we treat it as separate from classical physics. This chapter shows that if you accept that all particles are waves with structure and spin, the quantum world starts to make intuitive sense. Wave-particle duality and other “mysteries” are natural outcomes of field behaviour.

Spin is not a quirky quantum property. It's the foundation of all physical motion. Planck’s constant defines the smallest unit of angular momentum, making it the heartbeat of the universe’s structure. Everything spins, and spin defines everything.

The Uncertainty Principle isn’t about fuzziness or confusion. It’s about the deep interconnection between motion and measurement. You can’t perfectly know a particle’s position and momentum at the same time because they're different faces of the same process. This chapter reframes uncertainty as a natural limit of structured fields.

Fields are more than mathematical abstractions. They are the basis of all of the physical universe. And there is only one type - Electromagnetic. This chapter lays the foundation for understanding how all energy, matter, and forces emerge from field dynamics.

What if charge and magnetism aren’t fundamental points but consequences of something deeper? Here we explore how electromagnetic fields give rise to electric charge and magnetism, opposing the current school of thought. It is the elegant interplay of these dynamic fields within the roton that create all of the forces in nature.

In this chapter, the structure of the electron is revealed. Made from two gamma-ray photons colliding at right angles, their energy locks into a spinning loop called a roton—a stable, three-dimensional wave. This motion gives rise to mass, charge, and spin, with no need for point particles. The electron is light, folded and locked into form.

This chapter shows how protons, neutrons, and electrons form from light itself, held together purely by the electromagnetic force—no need for a separate “strong force.” Through Structural Electrodynamics, we uncover the physical structure behind charge, spin, fusion, and the stability of matter itself.

From the subatomic to the cosmic, SED extends its insights to the vast structure and evolution of the universe. This chapter explores how time, matter, and space emerged through waves of creation, annihilation, and expansion - guided by electromagnetic fields. A fresh explanation for inflation, antimatter asymmetry, and mass reveals the universe as a dynamic interplay of field-based phenomena.

Gravity isn’t a force - it’s space itself compressing around matter, pulled inward due to its formation. This chapter redefines gravity as a geometric effect caused by the 3D twisting of energy, revealing the true link between mass, spin, and space-time. SED offers a physical explanation Einstein never had, uncovering why gravity is weak, always attractive, and utterly fundamental.

SED suggests that even the darkest forces in the cosmos (black holes, dark matter, and dark energy) emerge from the dynamics of electromagnetic fields. From accelerating expansion powered by ongoing annihilation, to invisible rotons that may comprise dark matter, this chapter offers field-based explanations where standard models fall silent. It even draws a provocative link between black holes and fundamental particles through the fine structure constant, hinting at a cosmic symmetry.

Maxwell’s equations are the foundation of electromagnetism, and SED brings them to life by modeling particles as dynamic, twisting field structures called rotons. Within this framework, electric charge emerges from divergence, mass arises from curl, and the dance between E and B fields sustains both light and matter. The roton isn’t just compatible with Maxwell’s theory - it’s a vivid physical manifestation of it.