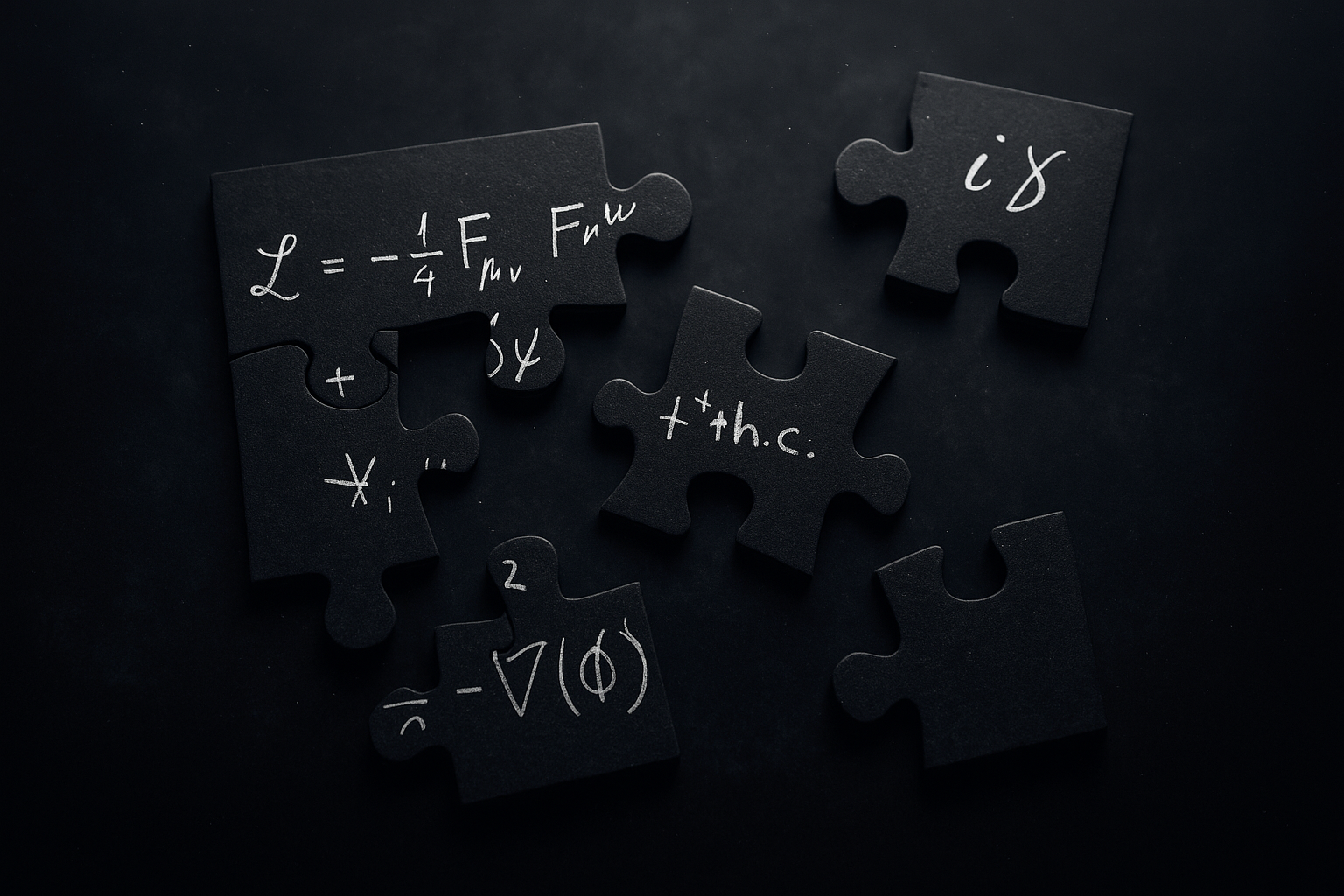Chapter 20
What is a Spinor?
The word "spinor" was first coined by Paul Ehrenfest in his work on quantum mechanics. However they were initially introduced into geometry by Elie Cartan in 1913. Spinors are an abstract mathematical entity, now deeply involved in our ideas of particle physics and similar branches of science, but so far have evaded all attempts to explain exactly what they are physically. Despite many efforts, they remain another elusive concept in physics. Even one of the greatest experts on spinors and their geometry, Sir Michael Atiyah, admitted he had no idea of what they really were, although their importance to science was critical, because they are somehow involved in the formation of matter.
This section will try to present some new light on spinors and help us understand how they create fundamental particles using classical or non-quantum physics. SED proposes that we now have a model that explains the structure of both the spinor and elementary particles. It is simple and beautiful and enables us to not only visualise a spinor, but to use this model to predict all the properties of fundamental particles and comprehend how matter is made.
Some properties of spinors
· A spinor transforms to its negative when the space it exists in, rotates through 360°. Currently physicists maintain this is not ordinary space but requires a special abstract or mathematical one. However, SED asserts real space is perfectly adequate with its model. (see diagrams below).
· It takes a rotation of 720° for a spinor to go back to its original state.
It appears that all fundamental particles in nature that are spin h/2 and described by the Dirac equation, have these properties.
Figure 38 - Above, a spinor visualized as a vector pointing along the Möbius band. [from Wikipedia article - Spinor]
Current ideas on spinors
This diagram, taken from Wikipedia, shows how spinors have until know, been thought of as a kind of Möbius band, exhibiting a sign inversion when the circle (the "physical system") is continuously rotated through a full turn of 360°. We see that a spinor is proposed to transform to its negative after the system rotates once. This is shown by the green and red arrows pointing in opposite directions. It takes another full turn, or double rotation of 720° for a spinor to go back to its original state and clear this inversion.
According to SED , this is not a very satisfying description of a spinor’s full behaviour, but is there a model can depict this better? One that enables us to imagine how a spinor exists.
SED and spinors
This section proposes one that has already been used to explain how elementary particles are created from energy, using only electromagnetic fields and their spin. The model is integral to a new branch of physics called Structural Electrodynamics or SED. The theory of Electrodynamics is well established in physics, being concerned with how light and matter interact, and SED contends that it is the physical structure of this process itself, at the elementary level when matter was made, that can guide us and explain from first principles what a spinor actually is.
We note that in the above description and diagram of a spinor, taken from Wikipedia, physicists use the concept of a mobius strip as the initial or base physical system. This is a curious object made from a strip that has a single 180° twist in its formation, before the ends are joined, thus giving it a single surface. Of-course this is an interesting structure, but SED contends: Why use it as a starting point if it cannot help us explain a spinor?
In SED’s model, we simply double the original 180° of twist to 360°, for each full rotation, as shown in the next diagram. With this change, we see that spinors can finally be visualised and have their properties interpreted physically. They are no longer the unfathomable mystery that only has meaning in abstract mathematics, such as orthogonal Lie algebra and Minkowski space. Simple geometry and mathematics, plus regular 3-D space are all that is necessary.
Here we show how to make the model of a spinor, by first twisting, then joining the ends of a length of plastic strip. This should be at least 50 cm by 1 cm and marked-up with E and B-fields, as shown in the second group of figures below. SED calls this structure a roton or rotating photon. In reality, rotons are made from a single cycle of an electromagnetic wave that consists of one Planck constant, or h, of spin. This has been described in more detail in the earlier section on Structural Electrodynamics. The following diagrams and text serve as a recap and are repeated here as this is an important topic, although it may be new and somewhat complex at first.
Figure 39 - Making a roton from a thin flexible strip. The roton is a spinor.
Figure 40 - A photon moving in the roton’s path creates all the properties of a spinor including charge, magnetism and mass. Modified from Williamson and Van Der Mark [5]
The curved, 3-D figure-8 shape in the diagrams above and below shows both the structure of spinors and the basic shape of all elementary particles. Spinors are fundamental to particle physics, and we can now see how they are made. It shows how a spinor transforms to its negative when the space rotates through 360°, before returning to positive after another, or 720° in total. Please refer to the next diagram (Fig 27, below), while reading the following description.
The top drawing heredepicts a single cycle of a normal electromagnetic wave, then, with the effect of a 360º twist drawn below it. When the ends are joined, it shows how the E and B-fields evolve due to this structure. Starting at the crossover, we traverse one loop and 360°, to pass through the crossover again, when the magnetic field becomes opposite or negative. This continues in the second loop until we reach the crossover again, when the magnetic field returns to positive. Therefore it takes a full rotation of 720°, for a spinor to go back to its original state. SED calls this model a roton and maintains it provides the structural basis for how matter is made from high energy light or gamma rays.
It can only form in a roton, with its unique shape that turns the field back on itself, twice each cycle, making matter from light and holding it in space.
Is the electron a spinor?
Today, there is a consensus among particle physicists that even though they do not currently know what either is, our science and mathematics point to the conclusion that the electron is a spinor. SED completely agrees and says that once we understand what one is, we will know the other. They go hand in hand. For now, we will only write a few more words using inductive logic to close this argument.
Conclusion
The electron is a spinor.
The roton is a spinor.
Therefore, the electron is a roton.
The Origin of Everything
(Online Edition)